Koni, bir düzlem içindeki dairenin her bir noktasının, düzlem dışındaki bir nokta ile doğru parçaları aracılığı ile birleşmesi sonucu elde edilen geometrik bir cisimdir. Koniler aslında bir dairesel kesitin yahut bir üçgenin kendi etrafında döndürülmesi ve tabanına dairesel bir şeklin yapıştırılması ile elde edilmektedir. Koniler, tabanlarına göre isim almaktadır. Bunlara örnek olarak dairesel koni, eliptik koni verilebilir. Konilerin alan hesaplaması ise diğer geometrik cisimlerden biraz farklıdır.
KONİNİN ALANI NASIL BULUNUR?
Koninin alanını hesaplamak için bilinmesi gereken bazı değerler vardır. Koni aslında bir dairesel kesit ile bir dairenin birleşmesi neticesinde elde edilmektedir. Yani iki geometrik şeklin bir araya gelmesi sonucunda oluşmaktadır. Bu nedenle koninin yüzey alanını bulmak için öncelikle ayrı ayrı koninin taban alanı ve yanal alanının bulunması gerekmektedir. Bunu bir şekil ile göstermek gerekirse;
Koni alan formülü= Yanal Alan + Taban Alan = π.r2+ 2.π.r.a
Koninin yüzey alanını bulmak için öncelikle koninin taban alanını, daha sonra ise yanal alanını bulmak gerekmektedir. Çıkan iki sonucun toplamı ise, koninin yüzey alanına eşittir. Yani koninin alanını bulmak 3 kademeli bir işlemle ancak mümkündür. Yapılacak olan işlemleri adım adım göstermek gerekirse;
1. Öncelikle koninin taban alanı bulunmalıdır. Koninin taban alanı bir daireden meydana gelmektedir. Bu nedenle konin taban alanı, dairenin alanının bulunması ile ortaya çıkmaktadır. Bir dairenin alan hesaplama formülü π.r2 şeklinde ifade edilmektedir. Bu formülde Pi sayısı sabit bir deperi, "r" birimi ise dairenin yarıçapının uzunluğunu ifade etmektedir. O halde koninin taban alanı formülü π.r2 ile hesaplanmaktadır.
Koninin taban alanı hesaplaması= π.r2
2. İkinci işlem ise koninin yanal alanını bulmaktır. Koninin yan yüzey alanını 2 şekilde hesaplanabilmektedir. İlk yol hazır bir formülü kullanmaktır. Yarıçapı "r", ana doğrusunun uzunluğu ise "a" olan bir koninin yanal alanı; 
olarak bulunmaktadır. Daha sonra ise yapılacak işlem koninin taban alanı ile yanal alanını toplamaktır.
3. Koninin taban alanı ile yanal alanı bulunduktan sonra yapılacak işlem bu verileri toplamaktır. Böylece koninin yüzey alanı elde edilebilecektir. O halde koninin yüzey alan formülü; π.r2 + 2.π.r.a olacaktır.
Lakin bazı durumlarda koninin yüzey alanını bulmak için farklı bir yol izlemek gerekebilir. Bu yol için gerekli olan bilgiler biraz farklıdır. Bu yol genellikle üniversite sınavlarında yahut sonrasında gerekecektir. Koninin yüzey alanı formülü
Bu formülü de bilmek önemlidir. Zira durumuna göre, hangi formülün kullanılacağı değişebilmektedir.
DİK DAİRESEL KONİNİN YÜZEY ALANI
Dik dairesel koninin yüzey alanı da, koninin taban alanı ile yanda bulunan daire diliminin alanının toplanması sonucunda bulunmaktadır. Dik dairesel koninin yüzey alanının bulunmasında trigonometrik denklemlerden faydalanılmaktadır. Daireler arasında oran olduğu için bu yol izlenmektedir. Yarıçapı "r", ana doğrusunun uzunluğu ise "a" olan bir dik dairesel koninin yüzey alanı şu şekilde hesaplanmaktadır:
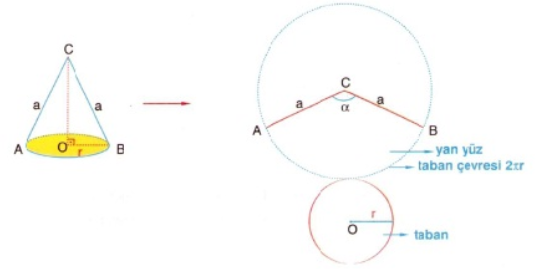
Dik dairesel koninin alanı= πra + π.r2
Burada önce tabanın alanı bulunmaktadır, ki taban bir daire olduğu için tabanın alanı π.r2 şeklinde bulunmaktadır. Daha sonra ise daire diliminin alanı bulunmakta ve çıkan değerler toplanmaktır.
KONİNİN KESİT ALANI
Koninin kesit alanı, koninin yer ile temas eden bölgesinin alanıdır. Koninin tabanı bir daireden oluşmaktadır. Dolayısıyla koninin kesit alanı, dairenin alanına eşittir. Dairenin alanı pi sayısı ile dairenin yarıçapının uzunluğunun karesini almak sureti ile bulunmaktadır. O halde dairenin alanı π.r2 olarak ifade edilmektedir. Koninin kesit alanı da, dairenin alanına eşit olduğuna göre; koninin kesit alanı formülü π.r2 yolu ile bulunmaktadır.
Koninin kesit alanı:
