Paralelkenarın Alanı Nasıl Bulunur? Paralelkenar Alan Hesaplama Formülü Nedir?

Paralelkenar, özel bir dörtgen türüdür. Bu dörtgenin karşılıklı kenarları birbirine paralel olup, uzunlukları da birbirine eşittir. Paralelkenarın 4 kenarı, 4 açısı ve 2 adet köşegeni vardır. Paralelkenarın köşegenler birbirlerini ki eşit parçaya ayırmaktadır. Paralelkenar, bir çokgen olduğu için iç açıların toplamı 360 derece etmektedir. Keza her çokgende olduğu gibi dış açıları toplamı da 360 derecedir. Paralelkenarın karşılıklı iç açıları birbirine eşittir. Bu nedenle paralelkenar, geometri sınavlarında sıklıkla tercih edilmektedir. Paralelkenarda neticesinde bir dörtgendir ve alanı buna göre hesaplanmaktadır. Aşağıda paralelkenar alan hesaplamanın nasıl yapılacağını bulacaksınız.

Paralelkenarın alanı nasıl bulunur?

Paralelkenar bir dörtgendir. Bilindiği üzere genel olarak dörtgenlerin alanı taban ile yükseklik uzunluğunun çarpılması ile bulunmaktadır. Bu açıdan paralelkenar da aynı formüle sahiptir. Lakin paralelkenar alan hesaplama formülünü uygulayabilmek için öncelikle paralelkenarın yüksekliğini bulmak gerekmektedir. Paralelkenarın alanı, yükseklik ile yüksekliğin indiği tabanın uzunluğunun çarpılması sonucu elde edilmektedir. Bunu bir resim üzerinden anlamak daha kolay olacaktır:

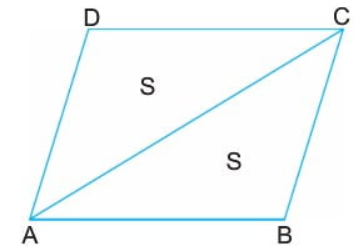
Paralelkenar alan formülü= a x h

Yukarıdaki şekilde bir paralelkenar verilmiştir. Bu şekilde "a" paralelkenarın bir kenarını; "b" ise diğer kenarının uzunluğunu sembolize etmektedir. Bu paralelkenarın yüksekliği ise "h" olarak gösterilmiştir. O halde paralelkenarın alan hesaplaması; a ile h'nin çarpılması ile bulunacaktır.

Paralelkenarın alanını bulmakta genellikle kullanılan yol; paralelkenarı bir dikdörtgene çevirmektir. Bir diğer yol ise alanı, paralelkenarı üçgenlere bölerek hesaplamaktan geçmektedir. Paralelkenarda farklı yükseklikler çizilebilmektedir. Bu sayede de paralelkenarın alanını bulmak için farklı yükseklikler kullanılabilmektedir. Zira elde edilen sonuç değişmeyecektir.

PARALELKENAR ALANI ÖZELLİKLERİ

Öğrencilerin sınavlarda işine yarayacak bir diğer husus ise paralelkenar alanı özelliklerini iyi bilmeleridir. Zira bu dörtgen kendine has birtakım özelliklere sahip olduğundan, alan hesaplamalarında da bazı işe yarar farklılıklara sahiptir. Paralelkenar alanı özelliklerinin bazılarını sıralamak gerekirse;

1) Paralelkenarın köşegenleri, paralelkenarın bir köşegeni, paralelkenarın alanını 2 eşit parçaya ayırmaktadır. Paralelkenarın iki köşegeni ise, paralelkenarın alanını toplamda 4 eşit parçaya ayırmaktadır. Bunu şekil ile anlatmak gerekirse;

Yukarıdaki şekillerden de görüleceği üzere, paralelkenarda köşegenlerle ayrılan yerlerin alanları birbirine eşittir.

2) Paralelkenarlarda alanla ilgili bilinmesi gereken bir diğer husus ise alanların oranıdır. Paralelkenar içerisinde üçgenin alanı, paralelkenarın alanının yarısına eşittir. Bu durumu bir şekil ile anlatmak daha kolay olacaktır;

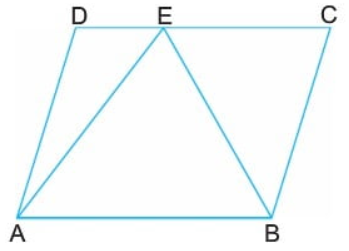Formül: A(EAB) = A(ABCD) / 2

3) Paralelkenar alanında dikkat edilmesi gereken bir diğer husus ise yine alan oranı ile ilgilidir. Paralelkenarın bir açısından çıkan iki doğru, paralelkenarın diğer iki kenarını ortadan iki eş parçaya bölüyor ise; bu durumda paralelkenarın alanı da 1-2-1 oranı ile üç parçaya bölünmektedir.

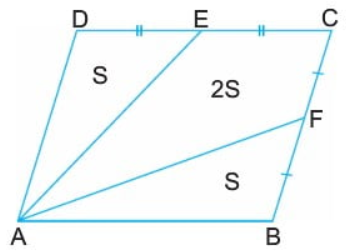Formül: A(DAE) = A(FAB) = A(ABCD)/4

Bu durum ancak E ve F doğruları, orta noktaya geliyor ise mümkündür.

4) Paralelkenarın alanında bir diğer özellik ise yine doğrular ile paralelkenarın parçalanması halinde ortaya çıkmaktadır. Paralelkenarın iki kenarı eş parçaya bölen ve bir üçgen oluşturan bir doğru durumunda, bu üçgenin alanı, paralelkenarın alanının 8'de 1'i etmektedir.

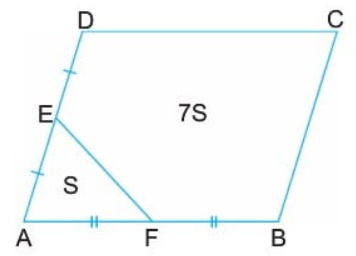Formül: A(AEF) = A(ABCD) / 8

Bu durum ancak E ve F doğruları, orta noktaya geliyor ise mümkündür.

PARALELKENAR ALANI ÇÖZÜMLÜ SORULAR

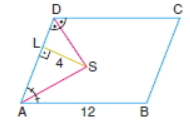
1. Aşağıda ABCD paralelkenarı verilmiştir. AS ve AD birer açıortaydır. SL doğrusu ise AD kenarına diktir. SL doğrusunun uzunluğu 4 cm, AB doğrusunun uzunluğu ise 12 cm'dir. Buna göre ABCD paralelkenarının alanı ne kadardır?

A) 122 B) 84 C) 96 (Doğru cevap) D) 100 E) 64

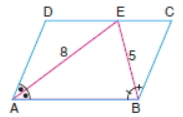
2. Aşağıda ABCD paralelkenarı verilmiştir. Bu şekilde AE ve BE birer açıortaydır. AE doğrusunun uzunluğu 8 cm, BE doğrusunu uzunluğu ise 5 cm'dir. Bu verilere göre, ABCD paralelkenarının alanı ne kadardır?

A) 60 B) 45 C) 50 D) 32 E) 40 (Doğru cevap)